Лига образования публикует результаты первого опроса преподавателей-предметников. Часть вопросов едины для всех предметников, часть носят специфический характер. Целью исследования является получение общей картины о состоянии преподавании школьных предметов с точки зрения педагогов и их оценки запросов современных детей.

По результатам первого опроса “Математика для современных детей” выявлены основные тенденции:

Только 5,8 процента от числа опрошенных педагогов считают, что их уроков достаточно для изучения математики.

Заниматься с репетитором дети начинают уже в начальной школе.

Большинство детей в обучении математики предпочитают самостоятельную работу, считают респонденты.

В математике почти треть учеников, по мнению опрошенных педагогов, интересует возможность улучшить свою финансовую грамотность.

Наиболее популярны среди педагогов специализированные сайты сделаны руками таких же педагогов.

Мы также попросили участников конференции “Математика для современных детей” прокомментировать результаты.

Выборка

Опрос “Математика для современных детей” проводился в виде онлайн-анкетирования в октябре-ноябре 2015 года среди пользователей сайта “Педсовет” (http://pedsovet.org), проживающих во всех регионах Российской Федерации. Большую часть опрошенных составили женщины в возрасте 25-55 лет. Выборка распределилась равномерно: треть проживают в большом городе, треть - в небольшом и другая треть - в сельской местности. Большинство работают в основной и старшей школе. Основная часть опрошенных используют учебники издательств “Просвещения” и “Мнемозина”. Большинство также знакомы с новой Концепцией математического образования, разработанной по заказу Правительства РФ.

Всего опрошено 378 человек.

Эксперты

Владимир Погодин, учитель информатики ГБОУ Лицей 1536, победитель конкурса лучших учителей в рамках ПНПО в 2009 году, автор серии брошюр для начальной школы "Математические разминки", соавтор серий "Математический тренажер" для 4-6 классов, соавтор книги "Справочные таблицы по математике".

Проблемы предмета

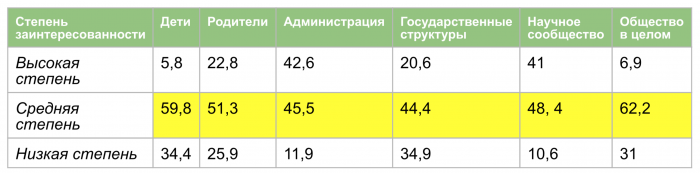
По мнению педагогов, наибольшую заинтересованность в предмете демонстрирует администрация образовательных учреждений. Почти половина опрошенных обозначили у своих руководителей высокую или среднюю степень интереса. Можно предположить, что это связано с повышенным интересом государства и родителей, который также отмечают респонденты.

Наименее заинтересованы в математике также государственные структуры (это мнение другой части опрошенных) и дети.

Тем не менее, если смотреть на все результаты по всем категориям, то интерес можно обозначить как устойчиво средний, а у детей - даже выше среднего. Возможно, жалобы на мотивацию (смотри ниже) можно отнести на “брюзжание”.

Низкую мотивацию детей в изучении математики отмечают больше двух третей опрошенных (74,5 процента). На втором месте по популярности (67,1 процента) ответ - “недостаточно времени на преподавание”. Значительно (64,5 процента) волнует также ориентация преподавания исключительно на сдачу экзаменов. Почти половина отметила недостаток необходимого оборудования.

Педагоги жалуются также на нагрузку, излишнюю отчетность и то, что не происходит смена поколений. “Мы просто уйдем и всё. Передать опыт некому”, - заметил один из респондентов в графе для свободных ответов.

Только 22 человека из всех опрошенных (5,8 процента) считают, что их уроков достаточно для изучения математики. Судя по данным опроса, дети интенсивно работают дополнительно. Одна треть занимается с репетитором, другая треть - самостоятельно. Почти двадцать процентов - ходят на подготовительные курсы и почти половина - в математические кружки. Большинство учеников пробуют свои силы в олимпиадах. Интересно, что заниматься с репетитором дети начинают уже в начальной школе.

Владимир Погодин: “Когда три педагога из четырех говорят о низкой мотивации у детей – что они имеют в виду? Предполагаю, низкое желание детей изучать предмет, который преподают эти педагоги и который в расписании назван «математика». Но «низкая мотивация» - настолько общее место, что на реальную проблему это тянет разве что по отношению ко всей школе. Да, детям не очень хочется учиться в нашей школе. И, подозреваю, не только математике. А проблема недостатка часов при обучении математике? Это общая проблема недостатка часов в принципе, практически по любому предмету. Проблема ориентации преподавания исключительно на сдачу экзаменов – чья? По сути это проблема не ориентации преподавания, а контроля за результатом. Учитель математики отвечает за результат, который показывают дети на единых внешних экзаменах. Прекрасно это понимая, он сам начинает ориентировать преподавание на экзаменационные задания, при этом причиной оказывается внешняя ситуация. Это феномен был исследован несколько десятилетий назад в странах, которые первыми начали вводить внешние проверки знаний обучающихся. Резюмируя три основные проблемы, можно их даже объединить: «дети не мотивированы, а мне недостаточно часов, чтобы готовить их к экзаменам». Другими словами, внешний мотив вытеснил внутренний, причем как для детей, так и для учителей. Естественно, падает заинтересованность в самом предмете. При этом интерес сдать экзамен может оставаться очень высоким”.

Интересы учеников

Большинство детей в обучении математики предпочитают самостоятельную работу. Более двух третей из них, по мнению педагогов, выбирают домашние задания в “решебниках”, а половина - решать примеры. Популярность же лекций преподавателей по числу процентов равны популярности обучения у одноклассников.

В математике почти треть учеников опрошенных педагогов интересует возможность улучшить свою финансовую грамотность и примерное количество (17, 5 и и 16, 4 процентов) нравится с ее помощью развивать мышление и логику. В свободном варианте ответа педагоги чаще всего называли - “ничего не привлекает”, “родители заставляют”, “надо поступать в вуз”.

Владимир Погодин: Вопрос – об интересах учеников – по сути характеризует скорее деятельность учителей, а не учеников.

Если половина учеников предпочитает решать примеры – значит, учителя этой половине учеников и задают решать примеры. Если больше 70 процентов учеников предпочитает ГОТОВЫЕ домашние задания в решебниках (а это значит, что они предпочитают ничего не делать, а просто списывать задания) – это говорит о том, что учителей ситуация дежурного выполнения таких домашних заданий устраивает. Если практически все учителя говорят о том, что дети не читают учебников и дополнительной литературы, значит, ни о какой самостоятельной работе детей не может быть и речи.

Опять же, если всего 13 процентов преподавателей считают, что ученики предпочитают учиться друг у друга, значит, в этих 13 процентах можно найти учителей, которые смотрят на взаимообучение позитивно. И если 14 процентов учителей убеждены, что ученикам нравится слушать лекции преподавателя, значит, не исключено, что хотя бы 14 процентов учителей такие лекции читать умеют.

Судя по общему низкому проценту, большинство учителей считает, что детей в математике мало что интересует. А финансовая грамотность – всего лишь модный тренд, учитывая, что современная школьная математика касается развития финансовой грамотности детей разве что в одном вопросе на экзамене.

Инструменты педагога

Компьютерные программы и электронные образовательные ресурсы предпочитают чуть более трети учеников. Примерно такое же количество используют специализированные сайты в интернете. Интересно, что компьютерные инструменты (например, симуляции) используют также около трети педагогов. Более популярными являются предметные курсы по выбору и игры.

Какие сайты наиболее полезны?

Участникам опроса был задан вопрос о наиболее качественных ресурсах в интернете, ориентированных на преподавателей математики. С большим отрывом в неформальном ранкинге победили сайты, созданные самими педагогами - сайт репетитора из Москвы Александра Ларина и учителя из Санкт-Петербурга Дмитрия Гущина. Среди названных сайтов также много ресурсов, созданных педагогами для педагогов и для учеников.

1

Сайт Александра Ларина

alexlarin.net

Решу ЕГЭ, Сдам ГИА

http://reshuege.ru/

2

Первое сентября

http://math.1september.ru

Федеральный инсититут педагогических измерений

http://www.fipi.ru

3

Сайт учителя математики

http://le-savchen.ucoz.ru/

Единая коллекция цифровых образовательных ресурсов

http://school-collection.edu.ru/collection/matematika/

ЕГЭ по математике

http://uztest.ru

4

Открытый банк ЕГЭ и ОГЭ по математике

http://mathege.ru, http://mathgia.ru

Фоксворд

http://foxford.ru

Карман математика

http://karmanform.ucoz.ru/

Меташкола

http://metaschool.ru

Московский центр непрерывного математического образования

Какие конкурсы наиболее полезны?

Около 16 процентов педагогов используют поточные соревновательные формы для своих учеников. Большая часть участвуют во всероссийской олимпиаде школьников на разных этапах, поэтому мы решили выделить негосударственные проекты, которые наиболее популярны среди опрошенных.

1

Кенгуру

https://mathkang.ru/

2

Вот задачка

3

Предметная сессия “Олимпус”

http://www.olimpus.org.ru/

Онлайн-олимпиада Фоксфорда

http://foxford.ru/o/olympiads

Электронная школа “Знаника”

http://znanika.ru/

4

Математический чемпионат (г. Пермь)

http://xn--80ajjpgff2a1byc.xn--n1adr.xn--p1ai/championships/

Турнир Ломоносова

http://turlom.olimpiada.ru/

Слон (Центр "Снейл")

http://nic-snail.ru/calendar/konkurs-igra-po-matematike-slon-2014

Ребус

http://konkurs-rebus.ru/

Меташкола

http://metaschool.ru/

У кого Вы бы хотели поучиться?

64 процента педагогов прошли за последние три года различные формы повышения квалификации. Многие отмечали, что прошли несколько курсов. Большая часть опрошенных прошла очную переподготовку по Федеральным государственным стандартам.

Лидерами среди операторов повышения квалификации ожидаемо выступили региональные институты повышения квалификации. При этом доля тех, кто прошел очную и дистанционную подготовку примерно равное. Лидерами негосударственного сректора среди тех, кто предлагает услуги в обучении педагогов являются Педагогический университет “Первое сентября” и Образовательный центр “Фоксфорд”.

На вопрос, у кого бы Вы хотели поучиться, был получен очень большой разброс фамилий, как живущих ныне педагогов, так и уже ушедших. Мы выделили список наиболее часто встречавшиеся фамилии действующих и поныне специалистов.

Ященко Иван Валерьевич

Директор Московского Центра непрерывного математического образования. Руководитель федеральной группы разработчиков ЕГЭ по математике. Учредитель Фонда "Талант и успех". Член совета при Президенте Российской Федерации по науке и образованию.

Мордкович Александр Григорьевич

Доктор педагогических наук, профессор Института математики и информатики МГПУ

Звавич Леонид Исаакович

Заведующий кафедрой математики гимназии № 1567 города Москвы. Народный учитель РФ, вице-президент российской Ассоциации учителей математики.

Смирнова Ирина Михайловна, Смирнов Владимир Алексеевич

Доктор педагогических наук, профессор кафедры элементарной математики Московского педагогического государственного университета.

Доктор физико-математических наук, профессор, заведующий кафедрой элементарной математики Московского педагогического государственного университета.

Шаталов Виктор Федорович

Народный учитель СССР, педагог-новатор

Владимир Погодин: Любопытно, что меньше всего проблем у учителя – в возможности своевременно повышать свою квалификацию. 64 процента педагогов при этом повысили свою квалификацию. Низкий процент констатирующих отсутствие проблемы в повышении квалификации в сочетании с тем, что только два педагога из трех повысили квалификацию за последние два года, может означать и то, что треть учителей не считает необходимым для себя повышать квалификацию.

При этом каждый третий учитель испытывает «сложности с внедрением государственных стандартов». Что это по сути означает? Государственные стандарты все-таки внедряются, но со сложностями, или государственный стандарт не осваивается учащимися, так как у педагогов сложности? К сожалению, формулировки ответов очень обтекаемые, что не позволяет нащупать проблему более предметно. Не исключено, что эти сложности испытывает как раз та треть педагогов, которая не повысила квалификацию за последние три года.

Метапредметные результаты

Наибольшее затруднение у опрошенных вызвал именно этот вопрос.

Одни участники затруднялись с ответом или отказались отвечать: «Умышленно пропущу ответ на этот вопрос», «Не нравится мне термин «Метапредметные результаты»», «Всё, что в примерных программах к ФГОС», «Для полного описания нужно много времени», «Тут трудно что - либо сказать конкретно, Отсутствие материальной базы делает внедрение ФГОС фикцией...».

Другие уклонились от личного ответа, вставляя однотипные формулировки рабочих программ по предмету и методичек.

Третьи склонны считать, что, поскольку математика используется в разных сферах жизни, то есть метапредметна по своей природе, то предметные результаты по математике являются одновременно межпредметными, метапредметными и общекультурными. «Математика вокруг нас (в окружающем мире, в экономике)», «Математика наука прикладная, поэтому почти все текстовые задачи являются метапредметными», «Математика формирует практически все метапредметные разультаты, только одни в большей, а другие в меньшей степени».

К сожалению, прошедший опрос не позволяет определить, с чем связаны затруднения с ответами на вопрос о личном опыте достижения метапредметных результатов и формальные ответы на данный вопрос:

– с обилием применяемых дидактических приёмов для достижения этих результатов,

- с личным нечетким пониманием различий между метапредметными, предметными и личностными результатами,

- с четким пониманием того, что разделение образовательных результатов на метапредметные и прочие – искусственно, формально, не существенно, является лишь требованием времени и современных нормативов, к языку которых нужно просто приспособиться (тем более, что ряд УУД можно отнести к нескольким группам результатов),

- с отсутствием реальной и наличием имитационной деятельности по достижению этих результатов, или с чем-то ещё.

Тем не менее, достаточно большое количество участников охотно делились своим опытом и высказывали сожаление, что не могут в рамках анкеты написать больше.

Какие метапредметные результаты формируются и могут быть сформированы на уроках математики?

1. Информационная грамотность, мышление, познавательные результаты (55 ответов)

«Развитие представлений о математике как форме описания и методе познания действительности», «Умения использовать математические средства для изучения и описания реальных процессов и явлений», «Использование математических методов в исследовательской деятельности», «Умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме», «Проводить классификации, логические обоснования, доказательства математических утверждений», «Способность к осуществлению логических операций сравнения, анализа, обобщения, классификации по родовидовым признакам, к установлению аналогий, отнесения к известным понятиям»,

«Умение разбивать задачи на подзадачи», «Умение думать, разбирать ситуацию "по полочкам"», «Умение выбирать и создавать алгоритмы для решения учебных математических проблем», «Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач», «Умение отрешиться от мелочей при решении проблемы», «Умение вдумчиво читать. «Использование знаково-символических средств представления информации: – чтение схем, таблиц, диаграмм;

– представление информации в схематическом виде».

2. Регулятивные результаты (27 ответов).

«Умение принимать на себя ответственность за результаты своих действий», «Умение соотносить свои действия с планируемыми, владеть навыками самоконтроля, взаимоконтроля», «Умения выполнять самоконтроль и релаксацию», «Умение оценивать правильность выполнения учебной задачи, собственные возможности её решения».

3. Предметные результаты по математике как межпредметные, метапредметные и общекультурные (22 ответа.)

«Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов»,

«Развитие способности видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни»,

«Связь математики с физикой, технической механикой, калькуляцией, электротехникой»,

«Умение решать экономические задачи».

4. Коммуникативные результаты (22 ответа)

«Решение коммуникативных задач с использованием речевых средств и информационных технологий:

– осознанное построение речевого высказывания в соответствии с задачами коммуникации;

– составление текстов различных типов (текст-описание, текст-повествование, текст-рассуждение);

– выбор доказательств для аргументации своей точки зрения»,

«Развиваю грамотную речь», «Совокупность умений по использованию доказательной математической речи», «Точно и грамотно выражать свои мысли с применением математической терминологии и символики», «Умения распределять роли, разрешать конфликты, находить общее решение, умения слышать партнёров и аргументировать и отстаивать своё мнение», «Умение сотрудничать с педагогом и сверстниками при решении учебных проблем».

5. Организационная и проектная компетентности (18 ответов)

«Умение самостоятельно ставить цели», «Умение самостоятельно ставить учебные задачи, планировать пути их решения», «Умение самостоятельно определять цели своего обучения, планировать пути достижения этих целей», «Умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности - систематическая работа по постановке такой проблемы, которая выводит учащихся на тему урока и на осознание необходимости ее изучения», «Умения планировать работу», «Планирование путей достижения результата», «Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера», «Учу планировать свою деятельность, ставить цели, выбирать алгоритм для достижения результата»,

«Проектирование», «Опыт проектной деятельности», «Программа самообразования».

6. Личностные (3 ответа)

Каким образом формируются метапредметные результаты на уроках математики?

1. С помощью современных образовательных, педагогических и социальных технологий, активных методов обучения и групповых форм работы (24 ответа)

«Работа в малых группах позволяет решить практически все дидактические задачи от изучения нового материала до закрепления и обобщения пройденного», «Работаем в парах, в группах, мозговой штурм, создание проблемной ситуации, игровые формы», «Технология проблемного диалога (структура параграфов)», «Развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии», «Перевернутое обучение»...

2. Через разноплановую работу с информацией (24 ответа)

« Учась решать текстовые задачи на математике, ребёнок может перенести это умение на другие науки – физику, химию», «Работа с научным математическим текстом, составлять план, опорный конспект и многое другое постоянно отрабатывается мною в ходе изучения предмета», «Ученики готовят доклады с использованием различных источников информации, создают презентации», «Индивидуальные проекты по истории математики, доклады учащихся, презентации», «Технология продуктивного чтения (задания по работе с текстом)», «Смысловое чтение - работа с содержанием учебника, поиск ответов на поставленные вопросы, применение технологии развития критического мышления и т.д».

3. Путём решения разного типа задач и наборов заданий (20 ответов)

«В рамках своего предмета, стараюсь решать задачи, связанные с реальными жизненными ситуациями», «Использую задачи из областей: географии, физики, экономики на проценты, вероятность и т.п.», «Пытаюсь формировать умение видеть математическую задачу в виде проблемной ситуации в окружающей жизни», «Нередко использую задания с самопроверкой или взаимопроверкой, что позволяет детям повышать ответственность за свои знания».

4. Через проектную и исследовательскую деятельность (16 ответов)

«На занятиях по проектной деятельности учащиеся готовят проекты по разным дисциплинам с использованием математического моделирования», «Через проекты, например: "Связь истории с математикой", «Проектная деятельность в урочной и внеурочной деятельности», «Научная работа, проекты, исследовательская деятельность», «Участие в НПК (научно-практической конференции) учащихся».

5. Через организацию целеполагания, планирования и оценки деятельности (15 ответов)

«Целеполагание, через постановку проблемы к каждому заданию" зачем решаем, чему научимся?", планирование - через проектирование алгоритма решения проблемы», «Предоставляю возможность самостоятельно осознать цели учебной деятельности, выработать программу действий, определить условия выполнения, поощряю использование различных технологий, настаиваю на самооценке и рефлексии по результатам деятельности», «Регулятивные результаты - выстраивать необходимый план действий, корректировать деятельность», «Технология оценивания (правило самооценивания)», «Стараюсь строить уроки по ФГОС, т.е. со взаимооцениванием, самооценкой, обсуждением плана и алгоритма изучения темы урока. Внимание- структурировании информации, а также готовиться к изучению темы (что повторить, в чем были ошибки раньше), выделять главное, записывать схемами, включать ассоциации и всегда подчеркиваю, что эти подходы можно в любом предмете использовать. Вдумываться в правила и т.д.», «Контроль деятельности - что получилось, рефлексия деятельности - что делать, что бы получилось».

6. Системно - деятельностный подход (8 ответов)

«Деятельностный подход в обучении я использую с середины 80-х годов. Он позволяет научить учащихся учиться. Многие мои бывшие ученики применяют умения составлять опорные конспекты, проводить анализ, синтез и другие приёмы учебной деятельности в дальнейшей учёбе и удивляются, что не все студенты владеют подобными навыками. Я люблю свою профессию. Она научила меня творчеству: я - соавтор, я - режиссёр, я - исполнительница одной из главных ролей совместно с моими партнёрами - учениками интереснейшей пьесы "Учебный процесс"», «На уроках использую системно-деятельностный метод. Основные моменты урока: что еще не могу (или не знаю), чему необходимо научиться (узнать), как достичь цели, оценить результат работы», «Акцент делаю на формирование и развитие самообучения»

7. Проверка и самопроверка, контрольные работы и тестирование (6 ответов)

«Регулятивные результаты - само и взаимопроверка дз и сам работ,диктанты по истинности и ложности...», «Во всех видах самостоятельной работы», «Социально-трудовая компетенция формируется при решении контрольных работ, выработке навыков устного счёта», «Тестирование», «Одним из направлений применения метапредметных умений в математике является усиление прикладной направленности, т.е. появление целого пласта задач практической направленности. Такого рода задачи появились в итоговых контрольно-измерительных материалах по математике (ЕГЭ, ГИА), это задачи на умение использовать приобретённые математические знания в повседневной жизни. Данные задания позволяют развить метапредметные компетенции, показать связь математики с жизнью, что обуславливает усиление мотивации к изучению самого предмета», «ЕНТ- все свободное время» (ЕНТ – аналог ЕГЭ, Единое национальное тестирование в республике Казахстан).

8. При помощи интегральных уроков (6 ответов)

«Организуем интегрированные уроки», «Преподаю математику и информатику, поэтому имею широкую возможность интеграции одного предмета в другой. В занятиях в ФЗФТШ удается присоединить еще и физику», «Совместные уроки с информатикой и физикой», «Информатика и математика - моделирование задач», «Интеграция математики и других дисциплин естественно - научного цикла».

9. Путём убеждения и повышения учебной мотивации (4 ответа)

«Привожу примеры применения математики в физике, экономике», «Объясняю непосредственно, как используется математика. Какие темы используются в физике, какие в химии, какие в экономике , какие в архитектуре , какие в строительстве , какие помогают развивать язык и что в целом математика учит логическому мышлению и коммуникабельности в жизни», «Повышением мотивации учащихся через включение жизненных ситуаций».

Цитировать

тег: Интересно